すべてのカテゴリ
新着有料ブログ
236 件中 1 -
60 件表示

4月ダッシュが大事な3つの理由
2024年度が本格的に始まりました。新中1生や新高1生は入学式や宿泊研修などに追われて、なかなか落ち着かない日々が続いているかもしれません。4月末から5月初旬にかけては約一週間の大型連休が控えており、学習ペースを調整したり、分からなくなった単元をまとめて復習するのにちょうど最適な時期です。言い方を変えると、ゴールデンウィーク中に態勢を立て直すことができなければ、そのまま夏休みに突入してしまうおそれもはらんでいます。学年が上がった場合も、急に授業内容が難しくなったり、先生が替わって授業がわかりにくくなったりして、調子を崩しやすい時期でもあります。春のスタートダッシュをうまく決められるかどうかは、この一年間の学業成績を占う上で非常に重要になってきます。4月~5月連休中は私もいくつかの特別授業講座を準備して、意欲ある中高生に学びの場を提供します。準備ができましたらお知らせします。今の時期は比較的授業枠に余裕がありますので、私の授業を受けてみたいという方がいらっしゃいましたら、ぜひお問い合わせください。
0

【数学】中学1年生で得意・苦手の分岐点になる分野
こんにちは!ゆんすけです!私は大学まで数学を学習をしていて、ずっと得意でした。学生時代の経験・家庭教師での経験から私が感じた、中学1年生で学ぶ内容で得意・苦手になる分岐点になる内容を書きたいと思います。中学1年生で学ぶ全内容①正負の数:数の大小、絶対値の概念を学ぶ、はじめてマイナスの概念を学ぶ。また、加減乗除や素数、素因数分解を学びます。②文字式:文字式での表し方、文字式の代入や加減乗除を行なう。③一次方程式:一次式の方程式を解きます。今後、「連立方程式」「二次方程式」を学んでいくので今後の基本になるもの。④比例・反比例:今後学んでいく、「一次関数」「二次関数」の基本となる分野。比例とは反比例とはなにかを学んでいく。⑤平面図形:直線と図形、図形の移動、基本の図形、円とおうぎ形を学びます。⑥空間図形:立体と空間図形、空間における平面と直線、立体の構成、立体の体積・表面積を学びます。⑦データの分布:度数分布表、ヒストグラム、相対度数を学びます。得意・不得意の分岐点になる分野①正負の数今後の数学を学ぶに当たっての基礎になる分野になるので重要です。特にマイナスが入った加減乗除が得意・不得意の人に分かれます。はじめて学ぶ概念でもあるが今後の数学の基礎中の基礎なので分からないところがあればすぐに潰しておかないと今後、数学が不得意になっていしまいます。④比例・反比例先ほどに書いていたとおり、中学2年生・中学3年生の時に学ぶ内容になる一次関数・二次関数の基本となる分野になるのでこの内容をしっかり抑えないと今後、不得意になる。この内容に関して最も理解欲しいものは、式の形とグラフの概形がどのように
0

【祝】合格でました、その2
前回の記事に続き、またしても嬉しいお知らせが。国立理系志望の生徒さんから合格のご報告がありました!Bさん(高3生)と初めてお話ししたのは秋ごろでした。その時点では、状況的には結構危険でした💦数学と化学を教えていましたが、やはり初めてみる問題と対峙した時に動揺してしまったり、いつもできていることを取りこぼしてしまうことが多く、なかなか点数が安定しないでいました。私がいつも受験生に言っていることがあります。それは「良くも悪くも、1ヶ月やそこらで人間の能力は劇的に変化しない。それよりも、自分の持っている能力をまずは出し切ることに集中しなさい。まずは、問題文を丁寧に読む。普段できていることを丁寧にこなす。できなければさっさと次に行く。難しい問題にかじりついて時間を空費するより、できることだけ着実にやる。それが「出し切る」ということだよ」Bさんにもそれをたくさん伝え、実践してくれました。上を言い出したらキリがないけど、まずは基礎がいかに大事かと言うこと。それが結果に結びついて、とても嬉しいです。今年も新たな生徒さんに会えるのが楽しみです!
0

【祝】今年も合格者出ました!
この時期になると、受け持った生徒さんから嬉しいご報告をいただくことが増えます。つい先日もいただきました!昨年の夏頃から、化学を教えていたAさん(高校3年生)。最初は本当に化学が苦手すぎて、何から手をつけたらいいのかわからない状況だったそうです。志望校合格に向けて、毎週毎週コツコツとビデオチャットで授業させていただきました。私が口を酸っぱくして教えたのは・文科省発行の教科書を最大限に活用すること・教科書やセミナー化学を活用した復習・検算の心得・解答スピードアップのコツ・暗記のコツ・暗記をしないで乗り切る方法などなど。教えられることは全て、注ぎ込みました。すると、Aさんの真摯な努力もあり、ぐいぐい力が伸びていったのです。本当に見違えるようでした。あとでお母様に聞いてびっくりしたのが、Aさんにとっていつの間にか化学が「大好きな教科」になっていたということ。あれほど苦手で、成績も底辺だった教科が、です。最後には「化学は面白い」「もっと勉強してみたいと思う」とも言ってくれていたようで、教師冥利につきます…!結果的に、化学が数学や英語を超えて一番得点力のある科目になったそうです。そして、志望校合格を勝ち取ってくれました…!本当におめでとうございます。先日、こんな直筆のメッセージを寄せてくれました。Aさんにはこれからも学び続け、成長し続けていって、いつか誰かの力になってほしいと思います!!本当にありがとうございました。それでは、また次の授業で!
0

都道府県立高校の入試シーズン突入!
3月に入ると、各都道府県立高校の入試シーズンに入ります。すでに試験が終わったところもちらほらあるようですが、3月5日前後に例年試験が行われている県が多いです。全国高校入試問題正解(通称電話帳)を開いてみると、各自治体ごとに個性があり、解いていてなかなか楽しいものです。私が住んでいる大分県は、全国でも数学の図形の問題が難しいことで知られています。この一年は自分が住んでいる県の中学生を教えていなかったので、なかなか県立高校の問題に触れる機会がありませんでしたが、今は授業が少なくて比較的時間があるので、過去問を皆さんに紹介してみようと思います。問2の(2)がなかなかの曲者です。もしかしたら一瞬で解ける解法があるのかもしれませんが、答えを出すのに少し時間がかかりました。それ以上にパソコン上で図形を描画するコマンドをすっかり忘れてしまっていて、うまく画像にできるまでに2時間もかかってしまいましたが。皆さんもよかったら挑戦してみてください。
0

最強の数学勉強法の1つ「BTKS」
こんにちは!短期間で数学の成績を上げるすごい勉強法、知りたいですか?…なんだか詐欺みたいですね(笑)でも、これは詐欺ではありません。・計算はできるけど、記述が書けない・解説を読めばわかるのに、自分では書けない・たくさん練習しているつもりなのに、テストで点が取れないこういう生徒さんは、たいてい「形だけ暗記」して問題を解いています。なので、違う形の問題が出てしまった瞬間に思考停止→お手上げになるのです。きちんと点数に結びつけるには、表面的な暗記数学ではなく、「BTKS勉強法」がおすすめです。1人でできる勉強法ですし、これを繰り返すと間違いなく理解が深まります。そして応用問題にも怯まなくなります。…って、BTKSが何の略なのか?この続きは体験授業でお伝えします。それでは、また次の授業で♪あずまひろ
0

【YouTube更新】線形代数 ~行列の和・差・積~
動画のご視聴・またcoconalaをご利用頂いている皆さん
いつもありがとうございます!
YouTubeを更新しましたのでお知らせです。
今回の動画は線形代数の超入門編です。線形代数と言えば行列!行列を知らない、線形代数を勉強した事がない、という方でもこの動画を見れば・行列とは何か・行列の和・差・積の計算が理解できる様になります。線形代数の世界への入り口となる動画です。ぜひ最後までご視聴ください。またcoconalaでの解説依頼も受け付けておりますので
お気軽にご連絡ください^^
0

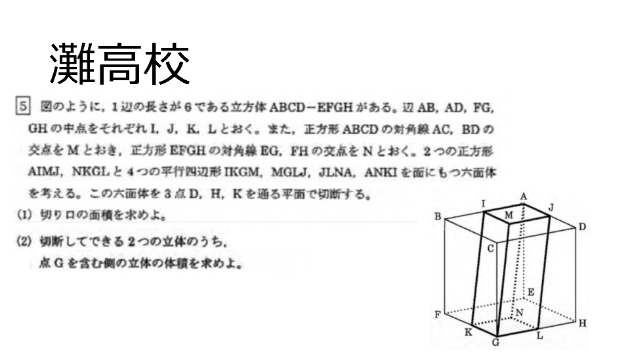
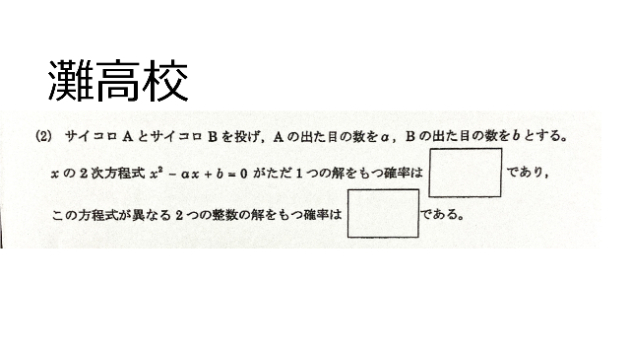
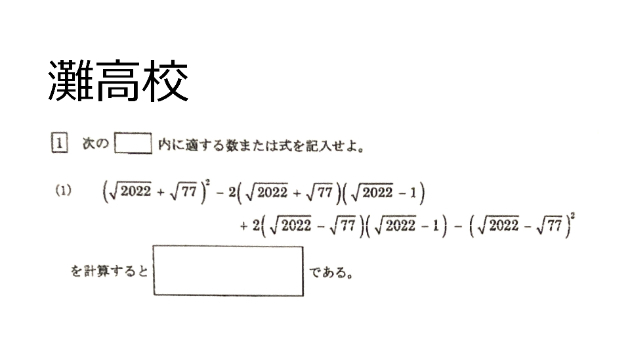
R4年度 灘高大問6
今日は灘中入試1日目です。受験者の皆さんの検討を祈ります(ラ・サール入試前の校内放送風)。一方、2月10・11日の灘高出願者は1月13日午後3時時点で130名。出願締め切りはまもなくですが、今年は何名受験するんでしょうか?灘の証明問題は、図に書き込んで証明ができるので親切設計ですね。やるべきことは割と掴みやすいですね。ただ、図が複雑なのでどこの共円点を見ていたのか混乱しました。
0
『芸能人格付けチェック』における確率
元日の能登半島地震の影響で休止となっていた、『芸能人格付けチェック』2024年お正月スペシャルが1週間遅れの、1月7日に放送されました。 基本ルールは『人気者でいこう!』の企画の1つだった、2000年代初頭と全く同じですが、2010年代中期からは2択だけでなく、3択の「絶対アカン問題」や、「絶対ありえへん問題」が登場しているため、「映す価値なし」になって画面から消えてしまうリスクがより増大しています。 その代わりに、最終問題の直前で「普通芸能人」だったチームが、最後の3択問題に正解すると、「一流芸能人」に復帰できる救済制度も設けられています。 「一流芸能人」or「映す価値なし」の確率は? では、「一流芸能人」で終わる確率と、「映す価値なし」となって画面から消えてしまう確率はどうなのか? その確率を、これから計算していきます。 なお、元号が令和に代わってからは、3問目が3択の「絶対アカン問題」と、最後の6問目が「絶対ありえへん問題」となっていますが、2024年の正月は企画の開始から25周年ということで、5問目も通常の2択ではなく、3択の「絶対アカン問題」となっていました。 これを踏まえると、計算の条件は以下のようになります。 <条件> ①:最初は全員「一流芸能人」からスタートするが、不正解の度にランクが「一流芸能人」→「普通芸能人」→「二流芸能人」→「三流芸能人」→「そっくりさん」→「映す価値なし」に下がってしまう。 ②:1問目と、2問目と、4問目は2択→正解なら現状維持、不正解を選ぶと1ランクダウン。 ③:3問目と、5問目は3択の「絶対アカン問題」→正解なら現状維持、不正
0

【YouTube更新】微分方程式 ~微分演算子を用いた解法~
動画のご視聴・またcoconalaをご利用頂いている皆さん
いつもありがとうございます!
YouTubeを更新しましたのでお知らせです。
微分演算子を用いた微分方程式の解法について解説した動画です。
coconalaで微分方程式に関する解説依頼を多く頂いておりますので、シリーズ化した9本目の微分方程式動画です。シリーズの動画を順にみて頂ければ基本から応用まで幅広く対応できる様になります。ご視聴よろしくお願いします!
またcoconalaでの解説依頼も受け付けておりますので
お気軽にご連絡ください^^
0

R4年度 灘高大問4
「PASSの確率」ですね。灘高は英進館の受験動員で福岡(その他九州)からの受験者が圧倒的に多いです。(灘高のH.P.に地域別受験者数と合格者数が載っています)。合格者数を受験者数で割ると、ざっくり50%くらいなので、求めた確率よりはPASSできますね。(灘高を受験するレベルの生徒での話ですが…)
0

思い込みではなく正しい認識をする!【アラフィフ心理カウンセラー「うさぴょん」のココナラ電話相談】
成功には様々な要素が絡み合いますが、その中でも特に重要なのが正しい認識です。何事も、誤った思い込みや曖昧な状態で進むことは避けるべきです。成功に向けて毎回最高の結果を出すためには、明確な指示と不明な点があれば積極的に質問することが欠かせません。
まず、自分のタスクや目標に対して思い込みに陥ることは避けるべきです。何かを達成する際、主観的な意見や過去の経験に基づく思い込みは、正確な判断を妨げることがあります。代わりに、客観的かつ事実に基づいた情報を求め、それを元に計画を立てることが成功への近道です。
指示が曖昧な場合、進む前にはっきりとした指針を確認することが大切です。曖昧なまま進むと、時間と労力を無駄にするだけでなく、誤った方向に進んでしまう可能性もあります。遠慮せずに質問し、確認することで、効率的にタスクを遂行することができます。
さらに、情報が不足している場合も、しつこく質問することが重要です。正確な情報が揃っていない状態で進むと、後で問題が発生する可能性が高まります。必要な情報が揃うまで確認を続け、基盤をしっかりと築くことで、成功への障害を最小限に抑えることができます。
結局のところ、成功への道は正しい認識から始まります。思い込みや曖昧な状態を排除し、明確な指示と十分な情報を得ることで、毎回最高の結果を生み出すことが可能です。成功には努力と計画が不可欠ですが、それを支えるのは正確な情報と的確な判断です。
0

年末年始の授業可能日程
2023年も年の瀬を迎えつつあります。公立の中高は今週末で冬休みを迎え、来年1月9日まで2週間ほどの冬休み期間に入ります。私が教えている私立の学校の生徒は既に冬休みに入っているところも多いです。大学受験生は共通テストまで一ヶ月を切り、受験生は毎日真剣に受験勉強に取り組んでいます。高校受験も早いところでは1月初旬に実施されます。この年末年始の過ごし方が合否を決めるのは言うまでもありません。この冬の年末年始の授業日程が大方固まりました。授業を入れられない日もありますが、12月31日から1月3日にかけては比較的余裕があります。また、そのほかの日程も、時間を選ばなければ授業を入れられる日があります。この冬休みに本気で学習に取り組みたい中高生、また、試験場で1点でも多く取りたい受験生、私は大歓迎です。お問い合わせいただければ、学習状況と将来の目標をお伺いした上で、この冬休みの間に最も学習効果の高い学習プランをご提案します。特に中高一貫校の中2~中3生は、この学年の成績が高3までずっと続くことが多いです。高校生の内容に入ると学習内容が難しくなり、遅れを取り戻すために必要な学習量も膨大になるので、ちょっとやそっとの努力では現状を変えることができなくなるからです。私は現在、中1から高3まで全ての学年の生徒を教えています。さまざまな地方に住んでいる生徒との出会いを通じて、私も学ぶことが多いです。この冬、大きく成長したい方をお待ちしています。授業可能な日程と時間帯12/25(月)19:00-23:0012/26(火)12:00-17:3012/27(水)18:00-23:0012/28(木)9:0
0

自分で解くことができました!
今日は少し気温が下がりましたが、それでも風も少なく比較的過ごしやすい一日でした。 今週は地域の小学校で懇談会が行われているようで、子どもたちの賑やかな声が聞こえてきましたよ。 さて、昨日の知識習得コースも皆、一生懸命勉強していました。 なかでも、証明を一から解くことに抵抗のあった中2生が、なんと自分で解くことができたんです! 「この問題は、この例題と似た解き方だから、嫌かもしれないけれど、例題を見ながらゆっくり自分で書いてみて。間違っていても良いので。」とお伝えしました。 するとしっかり書けていたんです。もちろん例題は参考にしたのですが、証明問題をいつも空白にしていたことを考えれば、もう充分です。 そのラボ生も何だかとても嬉しそうでしたし、おそらくこれからも少しは書いてみようと思ってくれるはず。 そんな様子を毎日見られることに感謝ですね。いつもありがとう!! それでは今日もゆっくりおやすみくださいませ。
0

直前期ほど伸びる! 直前期だから伸ばす!
2023年も残すところ一ヶ月になりました。時間の経過は本当に早いものです。24年春に大学を受験する皆さんは最後の追い込みの時期です。12月から1月にかけては、受験生が大きく2つに分かれます。緊張感を追い風にして集中力を高め、普段以上に学習効果を高められる人。それに対して、目前のすべきことに焦りから気を取られっぱなしになり、頭の中がスパゲッティになってしまって勉強に集中できない人。後者は開きもしない参考書や問題集ばかり買って精神を落ち着けようとするのが特徴です。前者の受験生は、これまでの学習の延長線上に「受験」というゴールがあるので、普段と変わることなくこれまで通りのことをやればよいだけです。後者の受験生は第三者が介在して取り組みを改善しなければいけません。焦っているだけでは試験で1点も獲得することができません。残り数十日というこの段階で、受験生が今すべきことは何か。問題集をやるにせよ、何からどのようにとりかかるべきか。直前期に入っても受験勉強の成果が上がっていないようでしたら、一度私に詳しい学習状況を問い合わせください。私から具体的なアドバイスをさせていただきます。
0

勉強ができる子、できない子のたった一つの違い
今回はこれまで300人、20,000回以上の指導をさせていただいたことで分かった勉強ができる できないのたった1つの違いをお伝えします!<読んでるか読んでないか>とってもシンプルですが「文章をちゃんと読んでるか 読んでないか」これだけです!「いやいやテキストは読んでる」と、思うかもしれませんが「読む」というのは「一言一句理解しながら読む」ということですこれが意外と難しいんです<答えはテキストにある>なぜかというと授業中の質問の内容や分からないことってほとんどがテキストに書いてあるんですよねもちろん質問することは素晴らしいですが書いてあることを読まずに質問したり読まずに止まってしまうことが多いのです<丁寧に読めば大抵理解できる>質問や止まった時「ここ一緒に読もうか」と、一緒に一言一句丁寧に読むとあ、そういうことか!分かった!となるんですこちらが教える必要ってあまりないんですよね<みんな勉強できる>「解説がしっかり載っているテキストを選ぶこと」これが前提ですが子どもはみんな自分で勉強する力を持っていますしもう少し丁寧に読めばもっと勉強できるようになるんです<丁寧に読んでもらう>なので「勉強ができない」と止まっている時はぜひ一緒にテキストを丁寧に読んでみましょう少し面倒に思うかもしれませんが子どもに頑張ってもらうにはまずは教育者側が頑張る必要がありますよね一緒に頑張りましょう!
0

グラハム数とは
グラハム数は、数学の世界で非常に特別な存在とされています。
この数は、アメリカの数学者ロナルド・グラハムによって1971年に紹介されました。
グラハム数は、非常に大きな数であるため、通常の方法で表記することは困難です。
その大きさから、グラハム数はしばしば驚異的な数と考えられています。
この数は、グラフ理論という数学の分野における特定の問題に関連しています。
具体的には、グラフの頂点を特定の色で塗り分ける問題、いわゆる「ラムゼー理論」において登場します。
グラハム数は、ある特定の条件を満たす最小の数として知られており、その数は非常に巨大であるため、人々の想像を超えています。
グラハム数を具体的に表現することは困難ですが、その大きさを理解するためには、階乗や累乗といった数学的な表現を利用することがあります。
しかし、それでもその巨大さを完全に理解することは難しいため、グラハム数は数学界において驚異的な存在とされています。
このように、グラハム数は数学の世界で特異な存在として知られており、その巨大さと複雑さが、数学者たちの間で広く議論されています。
グラハム数はギネスブックに載っている「証明に使われた中で最も大きい数」です。
数の大きさには限りがありませんが、「考察の対象になった数」として記録になっているそうです。
0

分数の割り算
お前は今更何を言っているのか?と思われるかもしれませんが・・・分数の割り算をあまり理解していません。解くことはできます。解き方は知っているので、すぐ解くことはできます。しかし、その意味がわかっていないのです。この話題については、同居の友達と年3日ほど毎年話し合います。というのも。割り算をピザで習ったんです・・・『1枚のピザを3人でわけるには?』と。で、それは頭で思い描くことができるんです。1枚を・・・3人だから・・・1/35本のコーラを5人でわけるから・・・1では、分数同士の割り算は?1/3のピザを・・・ここはわかります。1/3人でわける。1/3人・・・?1/3人って何・・・ここで頭に思い描くことができなくなるわけです。1/3を1/3個でわける・・・そう。『で、わける』と割り算を習ったからなのです。分数の割り算を考えるときに、1/3の中に1/3は何個『入ってる?』と考えると理解ができるんです。つまり、割り算は『で、わける』ではなくて『が、何個含まれる?』と読み解くと解けるようになるんです。これを掴むまでに人生ウン十年・・・でも、無駄なウン十年ではなかったと思います。悩み続けたからこそ、自分の中に納得のいく答えが出たわけで。こんな感じに、理解できないことでもゆっくりゆっくり紐解いて考えていけば、納得のいく解を求めることもできるんですよね。人生も同じです。難しいことがあったら、まず焦らない。じっくり考えましょう(*´ω`*)このメニューではこんな感じの雑談もできます。悩んだり、アレ?と思ったこと、共有していきましょう(*´ω`*)
0

算数(数学)の文章題が苦手で…
「算数(数学)の文章題が苦手で…」親御さんからもお子さんからもよく聞くお話です。 計算問題は順調に解けていても、文章題に入ると手が止まってしまっているお子さんが結構います。 そういう時に「まず、図や絵を描いてみて」と伝えるのですが、それすらも難しい。 長い文章を一度に頭で理解して解くのは難しいですが、文章に書いてあることを図や絵にしていくのはそんなには難しくはありません。 ただ、描けないのは図や絵にする練習をしていない(慣れていない)からだと思います。ですので、文章題が苦手なお子さんは、まず解かなくても良いので、文章を図や絵にすることを練習すると良いですよ。 それと、どれだけ生活の中で色々なことを経験しているかも大事だと思います。 例えば、6%の食塩水800gに水を加えて4%の食塩水を作る場合、何gの水を加えれば良いか。 という問題があった時に、例えばボールに入った6%の食塩水800gに、計量カップで水を入れているイメージが頭に浮かんで、あっ!食塩の重さ(g)は変わらないな〜と思えると、じゃあ食塩の重さでイコールにすれば良いかと問題を解いていける訳です。 他にもお買い物やお料理など勉強につながるものはたくさんあります。日々の経験を大切にしつつ、文章題克服のためにはまずは図(絵)にする練習をしてみてくださいね。 それでは今日もゆっくりおやすみくださいませ。
0

年末年始、本気の勉強しませんか?
2023年も11月中旬にさしかかり、入試シーズン間近になりました。推薦入試で既に合格が決まったという声もちらほら聞こえてきます。とはいえ、大半の受験生はこれからが本番です。最後まで気を抜かずに学習に取り組みましょう。私がオンライン授業を本格的に始めてからちょうど1年になります。開始当初に比べると授業のノウハウが格段に上がり、今では対面とほぼ変わらないクオリティーの授業を提供できるようになりました。学校の授業の復習や入試問題の過去問演習がなかなか進まないという方がいらっしゃいましたら、ぜひ一度私の体験授業を受けてみて下さい。11月末~12月初旬は生徒の各学校の定期試験期間にあたり、やや授業枠に余裕があります。また、年末年始は休まず授業を行います。塾が休みの日もしっかり勉強したい、冬休み中に実力をアップして3学期に臨みたい、高校受験や大学受験の最後の得点力アップに繋げたい、このような中高生や受験生にお薦めです。メインの指導科目は英語、数学、理科(化学・物理)ですが、国語をのぞく大抵の科目は授業可能です。また、医学部受験生などの小論文対策もお任せ下さい(国立大学医学部に合格しています)。まずはメッセージで現在の状況をお知らせ下さい。最も効率的な学習プランをご案内します。23年11月の空き日程カレンダーです。黄色い帯の部分が授業可能です。23年12月~24年1月については各ご家庭と現在調整中ですので、ある程度定まりましたら改めてお知らせします。
0

営業の基本:根性ではなく数学(確率)である
この記事は以下の記事の続きになります。30年以上昔の私が20代だった頃の営業は基本的に根性の営業でした。「受注するまで帰ってくるな!」と上司に発破をかけられ、闇雲に顧客対象の店舗や企業へ突撃訪問する、そんな時代でした。その時代の営業はまさに根性がある人が数字を作ることができた時代ですが、今はそんな根性論的な営業で受注を獲得することはできません。現在の営業は根性ではなく数学(確率)です。なぜ、営業が数学(確率)になったのか?をお伝えできればと思います。営業にはプロセスがある営業という仕事には受注獲得までのプロセスがあります。アポイント獲得↓商談↓プレゼン・デモンストレーション↓見積もり提示↓受注(成約)ざっくりと営業のプロセスを分解するとこのような流れになります。全ての業種業態において、この営業プロセスが当てはまる訳では無いですが、基本的にはこのようなプロセスを経て受注(成約)を目指します。30年以上前の営業では、例えば1日100件訪問しろ!と発破をかけられていましたが、なぜ1日に100件訪問しなければイケないのか?の根拠は示されませんでした。これは上司が過去の経験上で1日100件訪問したら、一定数の受注が獲得できるという経験値に基づいた一種の「勘」です。この「勘」の根拠となる数字を集計、分析することで効率的な営業を行うことができるのか?それを行うために営業のプロセスを見える化(可視化)し、数字(確率)に基づいた営業プロセスを実行することで、効率的に受注(成約)を獲得するのが現在の営業手法になります。よって、営業はまずプロセスを分解する必要があります。営業プロセスには一定の法則が
0

計算が苦手な大学生たち(教授)
これまで15年程度、大学生への授業をしてきました。東大生はおいといて、偏差値40~55程度の大学生への授業をして感じるのは 計算が苦手な学生が多い です。四則演算がメインの計算でありつつ、うまく計算できない学生が2〜3割いる印象です。日東駒専とよばれる大学群の経済学部でも、違う大学でもそうでした。一方、計算が楽勝にできる学生もいるので、変に易しすぎると、楽勝にできる学生には「こんなことばかりさせないでくれよ!!」と思われてしまうことも意識します。推薦入試が多様化したことによる弊害かもしれません。同じ大学/学部/学科であっても、大学生の学力は大きく異なります。楽をして大学に入っても、その後に苦労します。真面目にコツコツ、勉強しておくことは大切だと思います(計算に限らず、ですが)。
0

★算数で正しい時刻を!
今回は、算数の問題です!---問題---午前8時30分のとき8時39分を示していた時計が、この日の午後4時30分には4時27分を示していました。この日、この時計が正しい時刻を示したのは何時何分ですか。---解答---9/(9+3)=3/4(3/4)×8=6(時間後)
正しい時刻を指すのは、午前8時30分+6時間=午後2時30分---考え方---9分進んでいた時計が3分遅れにかわったということは、午前8時30分時点から午後4時30分時点までの遅れの合計が、9+3=12(分)になったと言えます。遅れの合計時間12分は、午後4時30分-午前8時30分=8(時間)8時間かかって一定の遅れで12分遅れたことになります。また、正しい時刻を示した時刻は、9分進んでいた時計が9分遅れた時点と考えられます。12分遅れの内9分の遅れは、9/(9+3)=9/12=3/4全体の遅れ12分の内で9分の遅れ分は、全体の遅れの3/4にあたります。算数で習った比例配分を使うと、
(3/4)×8(時間)=6(時間後)8時間の内6時間後の時点だけは正しい時刻と言えます。よって正しい時刻を指すのは、午前8時30分+6時間=午後2時30分となります。この問題の解法は、小学生が算数で習う比例の考え方になります。自分としては、算数や数学は思考訓練のツールであり、数や文字で表現された思考の言語かなとも思っています。(笑)/AI生成による画像/ /君をのせて/天空の城ラピュタ/井上あずみ / Studio Ghibli Cover/それでは、また次回。
0

誰に何と言われても 志望校は下げちゃダメ
誰に何と言われても志望校は下げちゃダメ「このままだと志望校は下げた方がいいですね」「志望校を下げた方がいいと言われました・・・」というお話をよく聞きますが・・・志望校は、絶対に下げちゃダメです!お願いだから下げないでください!志望校を下げてはいけない理由なぜかというと受験において最も学力が伸びるのは最後の1ヶ月間です私の生徒さんでは受験前の1ヶ月で偏差値が20伸びた子も実際にいます子どもの可能性って本当に計り知れない日々指導させていただいている中で私はいつもこう感じています志望校を下げたくなる理由そもそも、なぜ志望校を下げるのでしょうか?これは、「安心したいから」ではないでしょうか?・早く「受かる確約」が欲しい・不安な気持ちを落ち着かせたいこういった思いではないでしょうか?「不安になる気持ち」「安心したい気持ち」私も家庭教師を通して何度も受験を経験させていただいているのでこういった気持ちも本当に分かります志望校に100%落ちる時ですが、本当に可能性がゼロになるのは「志望校を下げた時」ですよね諦めない限り可能性はゼロになりません高校受験なら、公立高校でしたら基本的に試験は統一されていますそれなら学校によって対策を変えていく必要はありませんねだったら、願書を出すギリギリまで「行きたいところ」を狙い続けても問題ないのです大学受験なら学校によって試験が変わるので3年生の年末頃になったら改めて検討してみましょう志望校を下げるデメリット仮に、志望校を最後に下げるにしても「行きたいところ」を目指していた方が勉強のモチベーションも上がります「行けるところに行けるように勉強する」「ここに行きたい
0

Youtubeの動画、ガチ勉シリーズを公開しています。
こんにちは、進学塾twobeのハチこと大西です。うちの塾では、家で復習できるように、「ガチ勉」という勉強動画を配信しています。オンラインの授業がどんなものか、参考になると思います。オンライン授業の良い点はいくつかあります:
1. 柔軟性: オンライン授業は場所に縛られず、自分の都合に合わせて受講できます。通学の必要がないため、交通や移動時間を節約できます。
2. 学習のペース: オンライン授業では、自分のペースで学習できることが多いため、個別の学習スタイルに合わせて進めることができます。
3. 多様なリソース: オンラインでは多くのデジタルリソースが利用可能で、動画、オンラインテキスト、インタラクティブな教材などを活用できます。
一方で、オンライン授業には対面授業とは異なる課題もあります。いいとことばかりではありませんが、家で授業が受けられるなんて、最高じゃないですか。やるに越したことはないと思います。個人の好みや学習スタイルに合った形態を選ぶことが大切です。
0

子どもが勝手に勉強を始める3つの裏技
子どもが勝手に勉強を始める3つの裏技「勉強しなさい!」「もう怒るのも疲れた・・」子どもが勉強しないとついカッとしてしまいますよね結局お互いに消耗してしまいがちです感情で動かさないそんな時は感情ではなく環境で動かすことをまず考えてみましょう人は「環境」に合わせる生き物です勉強する環境がしっかり整えば自然と勉強するようになっていきます勉強しやすい部屋にする例えば家で何かに集中したい時テレビがついていたら集中しにくくて消したくなりますよね子どもにとっても今の環境はそもそも勉強しにくい環境かもしれません・勉強部屋にテレビがおいていないか確認・勉強机や椅子がちゃんとあるか確認・勉強している時間帯はスマホを預かる(テレビがあればテレビのコードを抜く)など、まずは部屋を整えましょう時間・タイミングを決める時間やタイミングを決めるのも、有効な環境設定です・平日はお風呂に入る前に30分勉強する・22:00-23:00は勉強するなど、子どもと話し合ってお互いに納得いく時間やタイミングを決めていきましょう親も一緒に作業や勉強をするこれが最高の環境設定です「まずは自分が勉強や仕事をしている姿を見せる」こうすることで子どもも真似して動いてくれるようになります「まずは自分から動くこと」これはどんなことにも通じる大切なことですね!
0

「やる気出して!」っていうとやる気がなくなる理由
「やる気出しなさい!」「やる気ないわね・・・」「やる気スイッチはどこ?」「やる気がない」というのは本当に悩ましいお悩みであると思います「結果よりも、とにかく 頑張って机に向かってほしい」といった声もよく聞きます「やる気が出てくれれば・・・」と思うのですが、今回はその「やる気」の正体についてお話しますやる気の意味とは?そもそも「やる気」とはどういう意味でしょうか?深く考えてみると「やりたくないことを 頑張ってやる」といった意味ではないでしょうか?例えば「遊びのやる気がある」とか「ゲームのやる気がある」とかは言わないですよね「やる気」ってつらいことをやる時に使う言葉だということが分かります辛いことをやりなさい「やる気出して!」この言葉を使うと「つらいことをやりなさい!」といった意味で相手側は受け取ってしまいますそれではモチベーションはなかなか上がりにくいですねじゃあどうすれば?感情ではなく環境褒めたり、叱ったり感情で動かすことも大事ですが人の感情は一時的なので長続きはしませんなので、感情ではなく環境で動かすことが一番効果的です例えば・勉強しやすい場所を 用意してあげる・勉強する時間や タイミングを決めて その間はスマホを預かる・親も一緒に勉強するこういったことです(詳しいお話は別の記事でしますね)家庭教師をつけるのも一つの環境設定ですね環境が整えばそこに合わせる勉強する環境が整えば子どもも自然と勉強するようになります(アフォーダンスといいます)そうすれば「やる気出しなさい!」という言葉を使ったり叱ったりして「こちらも疲れる」ということがなくなりますね「やる気」という言葉は使わず環境
0

子どもの頭 勝手に良くなる最強の質問
聞くだけで頭が良くなる質問「勉強しなさい!」「勉強しなさい!」怒るのも体力使いますよねできれば怒らず、勝手に勉強していってほしいものです怒らずに勉強させるそんな時は「怒る」のでなく「質問」しましょうそのフレーズがこちら「今日の数学、何勉強した?」科学的に正しい勉強法これ、何をしているかというと子どもが親に勉強を教えているんですねこれは、ラーニングピラミッドという学習定着率の図に基づいた科学的にも正しい方法なんですこのピラミッドの上部の勉強法ほど学習定着率が下がるんですよね実は「講義」は聞いた内容の5%しか覚えてないんです逆に「他の人に教える」はなんと90%!講義の18倍の効果がある勉強法なんですね子どもが先生、親が生徒なので、子どもに勉強を教えてもらいましょうそして、出てきた内容を深掘りしていきましょう「何勉強したの?」「確か一次関数」「一次関数ってどういうの?」「よくわからん」「じゃあ教科書でちょっとみてみましょ」こういった具合に一緒に学んでいくんです何も答えてくれない場合「知らん」「覚えてない」など、何も答えてくれないこともあるかもしれませんこの場合は「子どもが話してくれる」親子の関係性を目指していきましょうそういった情報も今後発信していきますね!
0

オンライン授業の受け付け準備中
こんにちは、進学塾twobeの大西です。進学塾twobeは、堺市北区と大阪市淀川区西三国にある個人塾です。集団指導と個別指導を行っています。今年度は塾長の指導枠に若干の空きがありますので、ご希望の方がいらっしゃるようでしたら、オンライン授業を受け付けようと思います、そのために現在準備中です。オンライン授業は当塾でも普段から行われています。雨が強く降って塾に来れないとか、微熱があって塾には行けないけど授業を受けたいとか、そういった場合に集団指導はオンラインで授業配信を、個別指導は個別でつないで授業をしています。大西の塾での指導歴は34年になります。多くの生徒を受け持ってきた経験を生かした指導と勉強のアドバイスをします。また、大西の娘は美術系の大学に進んでいます。大西本人も、美術や音楽などの文化的なことが趣味で、多様性やメンタルへの理解はあるほうだと思います。準備が整い次第、募集しようと思いますので、よろしくお願いいたします。それまで、大西の授業の様子をYoutubeにて見てみてください。「ガチ勉シリーズ」(進学塾twobeチャンネル内)
0

「ノーベル医学賞」って信用できない!
は?「ノーベル生理学・医学賞の受賞」が、あの最悪の「mRNAコロナワクチン」を開発した二人に与えられた。(^^;;;は??それって、ナニ??なんなの???今までボクは「ノーベル賞」って、とても名誉なことで、世界一の賞と言ってもいいくらいの気持ちでいたんだ。(^^;「世界一の名誉」と「一億円の賞金」と「最高のメダル」、それに「授与式」と「晩餐会(ばんさんかい)」という欧米では当たり前の「世界一の人間に対するおもてなし」じゃ。なのに・・・。なぜ???まあ、一応「コロナワクチン」により、多くのヒトが救われた?!となっているけどボクはぜんぜんそうは、思わないよ。(^^;「あんな、中途半端で、一年程度の最短?期間で”成功した?mRNAワクチン?”」って、それこそナンナン??????何度も言っているけど「臨床試験」って、必ずヒトに対する「治験」を実施しないといけないじゃんか!まずその前に「動物実験」なんかを何度も繰り返して、時間をかけてじっくりと検証するのが「通常」じゃ!そして「人間」に対しての「効果?」がありそうなら「老若男女、人種?」とかを色々と考慮して、「冷静、正確、誠実」に実験を行って、それを国家が「認証」するのが通例でしょ???(ーー;それがたった「一年程度?」での実験の結果じゃ。それに「副作用」もほとんど検証されてないよね。ま、無理じゃね。「圧倒的に時間が足りない」と思う。それなのに「ノーベル賞受賞」だなんて「狂気の沙汰(さた)」じゃ!(ーー;はじめてだよ~、ボクが「ノーベル賞」に疑問を持つなんて。まあ、「平和賞」とかってのも、なんかあやし~けどね。う~ん。まあ、許す。でも、「
0

受験本番が近づいてきました
このところ忙しくて、ブログ記事を更新できませんでした。2024年の共通テスト試験日(1月13日・14日)まで残すところ100日を切り、いよいよ大学受験生にとっては追い込みの時期に入ってきました。試験本番が近づいてくるほど、集中力が研ぎ澄まされてくるので、これから3ヶ月間は受験生にとってもっとも学習効率が期待できる期間です。合格を勝ち取るためにも、ここ一番しっかり気合いを入れていきましょう!理系受験生に多いのが、社会や国語(特に古文・漢文)対策を後回しにしてしまう人です。同様に、文系受験生は理科を12月まで伸ばし伸ばしにしがちです。のんびりしていると、除夜の鐘まではあっという間です。焦りが焦りを呼んで、暗記が全く頭に入ってきません。直前期に慌てないためにも、日程に余裕のある計画を立てて学習を進めた方がよいです。今年の年末年始は私も受験生を全力で支援するために、起きている間は全ての時間を捧げようと考えています。2024年受験生の方、あるいは再来年以降に受験を控えていて早めに受験対策に取り組みたいという高校生や中学生の方がいらっしゃいましたら、お早めにお問い合わせください。まだ未確定ですが、今年の年末年始は新規枠に限りがあります。事前にご予約をいただきましたら、現在指導中の生徒の日程が固った後、先着順に空き枠をご案内します。◆指導科目:英語、数学(高校入試、一貫校数学、数IA・数IIB・数III・数IIIC)、化学(物理は応相談)、世界史◆テーマ別:共通テスト対策、私大医学部入試対策、国公立大2次対策、中高一貫校フォロー、鉄緑会等進度の速い塾のフォロー
0

「悩みは”微分積分”で切り替えろ!」
ボクってねぇ~、前からず~っとある事件?で悩んで、思い切って爆発してやろ~とか、いいや、このまま耐えて時間の解決を待とうとか、まあ、20年以上?悩んでいたことあったのじゃ。「うん?もう考えないようにしよう・・・・・いや、なんか”ハラのムシが収まらないし!突撃するか?!いや、それは今できないぞ・・・いや・・・でも・・・」とか、とにかくグルグルと「無限ループ」という「地獄?」に落ちていたボク。;;まぁ、長いでしょ~!?ねぇ~(^^;詳細はこのSNSで前に何件か書いたので、知っているヒトは知っているとは思うけどね。(^^;;;それで・・・今の結論じゃ!それは・・・「微分積分」じゃ!!^^そう、それがボクの最終結論じゃね~♪とにかく悩み事や、心配事、それにイヤなことされての「ウラミ」、「ソネミ」、「復讐心」、「殺意」、「後悔」、まあ、たっくさんの「悪意?敵意?喪失感?」、とにかく書ききれないほどの「複雑な心」で「アタマがいっぱい」状態じゃよね。それでボクも前から「何かイイ解決法?」ってないのかなぁ~??って色々検索したり、ヒトになんとな~く聞いてみたりもしたけど、これが「なかなか解消法」ってないのじゃ!なにやらネットでも「お?これっていいかもよ!」と思った方法を試すというか、ちょいやってみたり、そういう「解消手段?とか思考方法?」なんていうのを、やってみたり、考え方を変えてみたりしたけど、これがなかなか「うまくいかないのよねぇ~」(^^;ま、そりゃ~、そういう方法って、その人のやり方だもん。ボクじゃ~ない!^^;それで、「これじゃ~、この悩み事に時間ばっかり取られて、人生つまらないな!
0

テキスト買っても勉強しない時に使える時間管理法
テキスト買っても勉強しない時に使える時間管理法「人気のテキスト買ったけど、全然勉強しない!!」前回、数学おすすめテキストをご紹介しましたがこれを買えば子どもは勉強のやる気が出てどんどん勉強するようになるでしょうか?・・・「ちゃんと勉強 したら苦労しない!」というのが本音、現実かと思いますなぜ勉強しない?人は基本的に24時間何かをしています子どもが家に帰ってもご飯を食べるお風呂に入るスマホを触るテレビを見るゲームをする寝るスケジュールは空いているようで子どもにとってやることは満タンなんです(子どもなりの 「忙しい」があるんですね)その状態でテキストを買っても勉強をやる時間が入ってこないんですじゃあ、どうすれば?最初に勉強する「家に帰ったら ご飯やお風呂の前に 30分勉強をする」これですご飯よりもお風呂よりも先に勉強するルールを設けましょう家に帰ったら最初に勉強するんです「勉強の優先度を上げる」ということもできますねこうやって子どもが勉強する「環境」を作ってあげるのです例えば、「貯金する!」となった時「余った分 貯金しよう!」と考えても基本的にお金は余らないですよね貯金したかったら【給料が入った時 最初に貯金する】これが鉄則ですよね勉強も同じで時間があるうちにやっておくのです「ご飯の前に30分やろう!」といった声かけを日々行う事で徐々に勉強の習慣づけができていきますとはいえ、「これで子どもが どんどん勉強するようになる!」という訳でもありませんこういった取り組みを「1つの要素」として捉えて1つ1つの積み重ねで徐々に変化していきます子どもに勉強を頑張ってもらうために教育者がそれ以上に
0

本当は教えたくない、プロが厳選した中学数学テキスト
本当は教えたくない、プロが厳選した中学数学テキスト数学全然点数取れない!数学のテストが白紙!学校の授業ついていけてない!「数学はどうやっても無理」と悩まれる親御さん、子どもさんは多いと思います本当は教えたくない最強テキストというわけで今回はプロ講師が本屋さんを巡って選んだ、「中学の数学テストで20〜50点の子が 自分で勉強できるようになり、 まずは60点代まで上げていける」レベルのテキストをご案内します!それが「ニューコース参考書」シリーズ!(※「問題集」ではなく「参考書」です)ネットでも書店でもお手頃で購入できメリット沢山の最強テキストですここではリンクが貼れないので、検索してみてください!何がいいの?メリット①「問題パターンが豊富」まず、掲載されている問題のパターンが豊富で学校ワークの問題集の問題はほぼ全て載っています「学校で分からなかった問題を このテキストで調べる」といったように、「数学の辞書」のように使うことができますメリット②「問題の前に必ず『例題』がある」これが「超重要」このテキストでは練習問題の前に必ず「例題」があり解き方を最初に学ぶことができますこの例題が「先生」の役割になり例題のお陰で子どもが自分で学べるようになるのです他のテキストだといきなり練習問題が並ぶことが多くこれでは子どもが「どう解けばいいか分からない」という心境になってしまい結果、やる気が損なわれます「まず例題で解き方を学ぶ」自主学習ではこれがとても重要になってきますメリット③「解説が豊富」練習問題の前の「例題」は答えまでのプロセスが細かく説明されていて解説がとても丁寧ですまた、解説中に「テストで
0

あなたの子どもさん、すでに倍率3億の入試に合格してます
「またテスト下がってるじゃないの!」「今回もスマホばっかいじって勉強もしてないじゃない!」テストの点数が下がり、勉強も全くしなかったそんな状況だと、「もうどうしようもないという状況!」と思うのも無理ないかと思います我が子を大切に思う分、「もっとやってほしい」という気持ちがどうしても湧いてきてしまいますよね以前の投稿で「点数が下がったら、頑張りを承認しよう!」ということをお伝えしましたでは、点数が下がって、頑張ってもいなかったら?そんな状態でも大丈夫です実はあなたの子どもは、既に3億人中の1位だからですどういうことかと言うと、「私たちは3億分の1の確率でここにいる」という事実がある、ということです人は生まれる前に受精のための戦いがあります1個の卵子に向けて、3億の精子が競争するのですまさに生死をかけた戦いですがそこで1位を取ったのが私たちなんです(妊娠にも確率があるので、実際はこれの数十倍低いです)「3億の競争に勝って生まれてきた」これを言い換えると、「倍率3億の入試に合格している」ということですこれって、「学年1位」よりも「東大理科三類に合格」するよりも、圧倒的にすごいことですよね「生まれてきて、今ここにいる」このことって実は、とてつもなくすごいことなんですもちろん「テストで点数上がってほしい」「勉強頑張ってほしい」という思いはあると思いますし、私もそのために日々サポートさせていただいていますしかし、子どもの成績で不安になった時「生まれてきてくれたことが素晴らしい」「ここにいることだけで素晴らしい」まずはこうやって考えることも大事ではないでしょうか?不安になった時は、「3億の壮
0

「このままだと行ける高校がない」問題、2秒で解決!
「テストの成績全然上がらない・・・」「学年順位がビリから数番目・・・」「このままだと行ける高校がない・・・」テストの点数や、学年順位の結果が衝撃的だと「このままだと将来、高校にもいけないんじゃないか?・・・」といった不安を抱えてしまうかと思います私もよく相談をいただきますし、子どもに「あんたこのままだと行ける高校もないよ!!!」と怒鳴ってしまった、というお話もよくお聞きしますこういう時、どうすればいいのでしょうか?お悩みの解決法教えます!事実:いける高校は100%ある子どもさん本人が「いきたい」と思っているなら、絶対に行ける高校はあります定員が割れている高校や、定時制など、調べてみれば、選択肢は必ずありますこれって、「行ける高校がない」訳ではなくて「選択肢が狭まる」という意味ですよね?確かに子どもの学力によって、選択肢の数は減りますしかし、ゼロではないですよね?重要なのは、「使う言葉を考えること」だと私は考えています「行ける高校がない」というのはご自身でお話を大きくしてしまっていませんか?ということです「行ける高校が全くない」訳ではないのに、そう言うことで、自分で自分の不安を大きくしていませんか?ということです「言霊」という言葉がある通り、言葉にはそれ自体に力がありますマイナスの言葉を使うと、マイナスが引き寄せられてしまいますよね「行ける高校がない」と言うだけで、より不安が湧いてきてしまいます「このままだと行ける高校ないわよ!」子どもにこう伝えることで、少しは勉強してくれるかもしれませんでもその時の子どもに、ポジティブな気持ちはあるのでしょうか?恐怖心から勉強することになってし
0

高校のテスト勉強 頑張りすぎると入試落ちます
「高校に入って学校のテストの順位が一気に下がった」「赤点取ってきた」高校に上がると勉強のレベルがまた更に上がり、成績が落ちてしまうことが往々にしてあります「このままだと行ける大学がない」「テストで順位半分くらいは取ってほしい」結果的にこういったご不安を抱える親御さまが多くいらっしゃいますが・・・実際の所、あまり問題ないです!むしろ「定期テスト勉強を頑張りすぎた」方が、志望校から遠のく可能性が大きいですその理由をお伝えしますね(※中学生の高校受験の場合は当てはまりません)ここは本当に引っかかることが多いのですが、大学の一般入試は「当日の点数」のみで決まります学校での成績は判断基準に全く入りませんここが本当に大事なことですなのでもう一度お伝えしますね!大学の一般入試は「当日の点数」のみで決まります学校での成績は判断基準に全く入りませんということは、学校の成績がどれだけ悪くても、そこは見られないから意味がないんですよね突き詰めて考えると、極論は・・・高校は順位がビリでも、赤点取りまくっても、謹慎処分になったとしても、高校卒業できて大学入試で合格最低点を超えられれば、全く問題なく大学合格できるんですもちろん、「高校が悪い」とか「高校のシステムが悪い」ということをお伝えしている訳ではありませんシンプルに、高校と大学が違う考え方を持っているんですよね定期テストの勉強が大学入試の勉強につながっているということはありますが「定期テスト=大学合格」という訳ではない、ということを「知っておく」必要があるんですそれぞれ別の対策が必要なんですね例えば理系大学を目指す子だったら、副教科はもちろんのこと、
0

「勉強しなさい!」→こう言い換えると勉強します
「勉強しなさい!!」「勉強しなさい!!」「勉強しなさい!!」と言っても微動だにしない・・・こういったことは日々起きていることかと思いますこの問題を解決するために①なぜこうなるか?②じゃあどうすればいいか?ということをお伝えしていきますね!①なぜ「勉強しなさい!」と言っても動かないのか→「何をすればいいか分からないから」例えば子どもから、「おいしいご飯作って!」と言われたらどうでしょう?「『おいしいご飯』ってよく分からないから、言うなら『何食べたいか』ちゃんと言ってほしい」こういった気持ちになるのではないでしょうか?子どもの心理もこれと似ているんですよね「勉強っていっても何すればいいか分からない」シンプルに、「何やればいいか分からない」というのが行動しない原因の一つなんですね②じゃあどうすればいいのか「勉強しなさい!」という言葉を、こう言い変えましょう「今日数学の授業でやったところを、ワークで解いて丸つけして!」やることを「具体的にして」伝えましょうこれで子どもも動きやすくなりますそしてこの伝え方は、具体的であればあるほどいいです今日数学の授業あった?何をやったの?そこはワークの何ページのところ?じゃあそこのページを、ご飯を食べたらやって!細かくすることでより行動しやすくなりますね基本的に日々の勉強は、・学校の宿題・日々の授業の復習を学校のワークでやるこの2つで大丈夫ですもちろん、「復習や受験対策」等、これ以外もやった方がいいことはありますが、ちょっと複雑になるのでここでは割愛します細かい所は塾や家庭教師にお任せしましょう「勉強して!」という言葉を「今日学校でやったところをワーク
0

オンライン家庭教師の3大メリット
コロナ禍をきっかけに流行り出したオンライン家庭教師ですが収束しつつある今でも非常にメリットのある受講形式であると言えます実際に親御様から寄せられているメリットを紹介します!1.送迎の手間がない・女の子なので、帰り道に心配しなくて済む・送迎などに気を取られないので、家のことに専念できる・そもそも塾が家の周りにない(沖縄から北海道、アメリカの生徒さまもご受講いただいています)多くの親御さまからこう言った声をいただいております家で受けられることで生徒さんの勉強時間する時間、親御さんの時間の両方が増えますね2.講師に365日いつでも質問できる家で勉強をしていて「これはどうだろう?」とふと疑問に思った時にすぐ聞けるから助かる、という声もいただいています(オンライン家庭教師ライフは、質問対応と解説動画作成を365日無制限でサポートしております)3.子どもが勉強を頑張っている姿が見れて安心する「時々部屋を覗くと、子どもが勉強を頑張っている姿が見られて安心します」と仰る方もいらっしゃいます「塾や学校だとどんな様子か分からない」というお悩みも、オンライン家庭教師だと解消できますね講師の目線から、4つ目の隠れたメリットも紹介します4.「自分の部屋」で学習する習慣が身につけられる「図書館へ行って勉強する」「学校に残って勉強する」こうやって、集中しやすい環境を変えて勉強するのも手ですが「どこかで勉強する」のは移動する必要がありますし、利用できる時間も限られますオンラインの授業を通して自分の部屋で勉強する習慣が付けられれば、どこか別の場所を利用するよりも、勉強時間がより確保できますねまた、自分の部屋で授
0

でき太くん三澤のひとりごと その44
投稿 その44三澤です。私がお子さんの学習をサポートさせていただく上で大切にしていることがあります。それは、明確な指導方針とカリキュラムの作成、そして状況に応じてカリキュラムを微調整する柔軟性と、最後まで子どもの成長を信じる意識。このことはとても大切です。この仕事をはじめたばかりの方と、指導歴が30年以上あるような方との決定的な違いは、上述した内容の質、対応の迅速さ、信念の深さではないかと思います。今、私の目の前に小学4年生で前学年の内容にかなり取りこぼしがあるお子さんがいたとします。(3年生までの計算にちょっとあやしいところがあり、文章題は2年生レベルまで対応可くらい)取りこぼしを補強せずに、このお子さんに4年生の内容を学習をさせることは学習にストレスを生じさせるだけでなく、「できない、わからない」という負の経験をさせることになります。これから算数に対する自信を取り戻そうとしている私たちにとって、負の経験をさせることはできるだけ避けたいところです。負の経験はどんどん子どもを萎縮させていくからです。このとき、もしおうちの方から「今度の学校の算数のテストで良い点数をとらせてあげたいので、わからないことを教えてもよいですか」というコメントがきたら、どのように回答したらよいでしょうか。回答例はいくつかあるかと思いますが、私は上述したくらいの取りこぼしの量のお子さんであれば、まずは学校のテストのことは脇に置いて、でき太の課題を優先するようにアドバイスさせていただくと思います。そして、取りこぼしさえしっかりと補強することができれば、テスト対策をしなくても、しっかり結果が出るようになること
0

★デザインのビジュアル効果
分数の性質をビジュアライゼーションしました。数だけの表現だと分数の概念を理解しづらいです。ビジュアルに置き換えて表現すると、その概念を認識できやすくなります。このようにデザインされたビジュアルは、理解を促進する効果があります。結局、全体の大きさが変化しないので分割の数を変化させても結果は同じ。という概念です。夜空ノムコウ/SMAP/hima.coverそれでは、また次回。
0

お母さんに一番やってほしいこと
子育てのノウハウって沢山ありますよね私もよく伝えています「存在を承認してあげるといいですよ」「他人ではなくて、過去のその子自身と比べて伸びたところを褒めるといいですよ」沢山ありますでもこれ、難しいですよね「分かってるけどついカッとなっちゃう」「それができないから悩んでる」これが正直なところだと思いますじゃあまずやるべきことって、これじゃないと思うのです「お母さん自身がまず心に余裕を持つこと」だと思うのです「まずご自身が満たされること」「ご自身の人生を生きること」このことを最優先すべきだと思うのですなので「家事や家のことをサボって休む」「自分を満たすためのリフレッシュを積極的にいれていく」ことをしてほしいのです「いやいや自分がやらないと大変なことになる!」となるかもしれませんご家族のために、やるべきことも沢山あるかと思います(私が想像している以上に、あると思います)ですがこういうのってちょっとくらいサボっても意外とうまく回ったりするものだと思います例えば会社だってカツカツ状態で急に欠員が出ても意外と普通に回ったりしますよね何でも「抵抗を感じるのは、事が起きるまで」だと私は考えています起きてしまえば意外と大丈夫だったりしますちょっとサボって自分だけの時間を作るリフレッシュする時間を作るご自身を大切にすることが、結果的にご家族のためになっていくと考えています子どもも意外と「自分が頑張らなくちゃ!」と思ったりしますよ
0

でき太くん三澤のひとりごと その43
投稿 その43毎日多くのお子さんの学習サポートをしていますと、時折「今日は子どもの気持ちがのらなかったようででき太くんの学習ができませんでした」というコメントをおうちの方からいただくことあります。大人でも気分がのらないことがありますから、この子のことは責められませんね。私にもそういうときだってあります。ただこのときに私たちが見逃してはいけないことは、「気分に左右されるような時間帯に学習時間を設定しているかもしれない」ということです。大好きなテレビ番組があと10分後にひかえているような時間帯遊びから帰ってきて疲れている時間帯運動系の習い事から帰ってきたばかりの時間帯夕食を食べたあとゆっくりくつろいでいる時間帯こういう時間帯だったりすると「気持ちがのらないこと」が起きやすくなりますよね。気持ちがのらないことが多くなると、学習は習慣化せず、習慣化しないと気持ちに左右されることがさらに増える。いわゆる悪循環です。この悪循環から抜け出し、気持ちに左右されない自分を作るには「習慣化を味方にする」と良いと思います。「習慣化を味方にする」にはコツが必要です。習慣化のコツは、すでに習慣化しているものの前後に取り組むことです。(私はできるだけ習慣化しているものの「前」に取り組むことをおすすめしています)多くの方が歯磨きを習慣化できるのは、寝るという行為の前に歯を磨くので、自然と習慣化していきます。朝、顔を洗うことが習慣化している方は、朝食前という必ず行うことに紐づいているため自然に習慣化していくのだと思います。でき太くんの学習についても、まずは完全に習慣化しているもの、必ず毎日することの前か後に、
0

プラチナランク達成!!(vol.17)
いつもご覧いただきありがとうございます!オンラインで算数・数学の家庭教師を専門にしておりますぺぬいと申します。
この度、ココナラプラチナランク達成いたしました!始めた時に目標にしていたプラチナランク。
今年の5月末にココナラに登録し、最初の1ヶ月の依頼は1件だけでした。
しかし、プロフィールや画像の改良を続けたことでご少しづつ依頼をいただき、6月末からコンスタントにご依頼をいただいております。
そしてココナラ登録から約3ヶ月、「プラチナランクになる!」という目標が達成できました!
数あるサービスの中、お目に留めていただきお声をかけてくださった皆様
サービスのお気に入り登録をしてくださった皆様
フォローをしてくださっている方々
いつも本当にありがとうございます!!
今後もお客様に満足いただけるサービスをご提供できるよう精進いたしますので、引き続きよろしくお願いいたします!
私は今年の3月に5年間勤めた高校教員を退職し、現在はオンラインの予備校で働いています。
教育の現場での経験をフルに発揮し、今後も活躍していきたいと考えていますので、今後ともよろしくお願いします!
0

でき太くん三澤のひとりごと その42
投稿 その42「思い通りにならないこと」生きていると、そういうことがありますよね。みなさんはそういうときどのようにされていますか。私の場合は、ちょっと気持ちを切り替えたり、捉え方を見直したりして乗り越えているように思います。もちろんそれだけでは乗り越えられないこともありますが、「生きていれば思い通りにならないことがある」ということは、だれに教わるでもなく自然に自覚するようになり、その対応方法も自分のペースで少しずつ身につけてきたのだと思います。振り返ってみると、私はその対応方法を遊びの中で身につけてきたように感じます。遊びといっても、オンラインゲームのような屋内の遊びではなく、屋外での遊びです。屋外は、夏であれば強い日差しと厳しい暑さ。冬は寒く、凍えることもある。晴れているときもあれば、曇りの日、雨の日もある。屋外に出た時点でもうすでに自分の思い通りにはならないことばかりです。癇癪を起こしても曇りが晴れになることはないですし、台風が自分のところだけを避けてくれることもありません。どうがんばっても自然を変えることはできない。思い通りにならない相手が自然という大きなものだと、もう順応するしか手立てがないのです。こういうことを「遊び」という楽しいことから身につけていくことが、一番ストレスのない学びなのかなと思います。自分が嫌いなことや、したくないことから「思い通りならないこと」の対処方法を学ぶのは、大人でもかなりストレスになるものですからね。私が心配になるのは、「遊び」の多くが屋内で、オンラインゲームのようなものばかりしているお子さんのことです。屋内は、屋外よりも「思い通りにならない
0

でき太くん三澤のひとりごと その41
投稿 その41私は週に3回ほど個別レッスンをしています。今、私がサポートしているお子さんで特に気になっているのは、現在中学2年生のお子さんです。私がそのお子さんにはじめて会ったのは、小学5年生の2月。このお子さんは、それまで通塾経験はなく、学校の宿題のみを行なってきました。その当時の算数の状況は、5+7や、12−5といった計算では指を使い、かけ算九九の暗唱では、6から9の段で間違えるところがいくつかあり、九九全体もスラスラとは暗唱できない状態でした。5年の2月でこの状況ということは、学校の授業は完全に理解できません。宿題もすべて解けない問題ですから、おそらくほとんど答えをうつしてしあげているという状態でしょう。ここでみなさんは少し疑問を感じませんか?学校では5年間、何をしていたのか?月曜日から金曜日まで毎日授業を受け、宿題をこなしてきたのに、5+7や、12−5といった計算では指を使い、九九がしっかり暗唱できないという状態。百歩譲ってこの子が若干奥手なお子さんだったとしても、5年もかけたらもっとレベルは上がっていてもよいのではないでしょうか。実際、私が2年近くサポートをしてきたことで、そのお子さんの算数、数学の状況は変わってきています。指を使う機会は減ってきていますし、九九も暗唱できるようになり、異分母の加減、小数などを理解し、今では正負の数の学習を進めるようになってきています。みなさんに今回のひとりごとでお伝えしたいことは、だれかの批判ではなく、最適化された学習プログラムの重要性です。2年でこれだけ成長するなら、もし5年かけたらどのくらい伸びていたのだろう。。。「この子の5年間
0

【YouTube更新】微分方程式_連立微分方程式 ~関数の置換え~
動画のご視聴・またcoconalaをご利用頂いている皆さん
いつもありがとうございます!
YouTubeを更新しましたのでお知らせです。
微分方程式_連立微分方程式の解き方について解説した動画です。coconalaで微分方程式に関する解説依頼が多かったので
動画も充実してきました。現時点で微分方程式だけで
8本目の動画になります。この8本の動画だけで
基本から応用まで幅広く対応できる様になります。
ご視聴よろしくお願いします!
またcoconalaでの解説依頼も受け付けておりますので
お気軽にご連絡ください^^
0

テストの点下がっても順位上がることあるってほんと?
テストの点下がっても順位上がることあるってほんと?〜〜〜〜テストが終わったのに、しばらく経っても結果が渡されない。こちらが聞くと、ちょっと緊張した表情でテストを持ってくる・・・。「・・・」また下がってるー!!!〜〜〜〜どれだけテストで頑張っていたとしても、テストの点数が下がっていると感情的になってしまいますよねでも実は・・・テストの点数下がっても順位が上がることがあるんです!なので、もう一歩踏み込んでテストを見てみましょう例:1学期中間テスト 60点1学期期末テスト 50点これを見ると「10点も下がっとるー!!!」と思うかもしれませんですが、これよりも見るべきところがありますそれは、『平均点』です!先生が平均点を出してくれているなら、テストの点数の横に「平均点」も記録しておきましょうさっきのテストは、もしかしたら・・・1学期中間テスト 62点 (平均点75点)1学期期末テスト 51点 (平均点55点)点数が10点下がっていても、平均点は20点下がっていたのかもしれませんこれはどういう意味かというと、「みんなが20点下がっていたのに対して、自分は10点しか下がっていなかった」ということですこれ、相対的に見ると順位は上がってるということなんですよねこのように、10点下がっても順位が上がることは全然ありえるんです「テストの点数」は、インパクトが強いですそれを見るだけで叫ぶくらい喜びたくなったり、泣きたくなるくらい悲しくなったりしますですが、「表面上だけでなく、一歩踏み込んで自分の子どもを見てみる」そうすると、いい事に沢山気づけますよ!オンライン家庭教師ライフ
0

9月以降の授業枠も少なくなりました
8月もそろそろ折り返しの時期になってきました。私の授業は来週までがピークで、8月21日以降は授業枠に余裕が出てきます。そろそろ9月を見据えた授業を考える必要があります。現時点で新規授業を受け入れられるのは、以下の通りです。月:17:00~19:45火:21:00~水:19:30~21:00木:21:00~金:×土:朝~17:00、20:30~日:終日(週によって流動的)また、各曜日とも午前中~夕方までは基本的にご希望の時間帯で授業が可能です。社会人の方で学び直しを考えていらっしゃる方や通信高校の在学生の方、海外にお住まいの方で時差を考慮する必要がある方にオススメです。今後入試シーズンが近づくにつれ、さらに枠が少なくなっていく可能性が高いです。オンライン授業に関心がある方がいらっしゃいましたら、お早めにお問い合わせください。また、9月1日以降から新規に授業を開始する場合は、授業料を改定する予定です。
0
.png)
夏休みも中盤戦!1学期の復習を一緒にしませんか?(vol.11)
夏休みが始まって2週間ほどが経ちました。気がついたら8月になりましたが、夏休みの宿題は順調に進んでいますか?1学期の学習内容をしっかりと復習して、新しい学期に向けての準備を進めるのは大切なことです。私は専門的に数学の指導を行っており、夏休みを利用して数学の学習を進めたいと考えている方々に対して、オンライン個別指導を提供しています。
夏休み中の時間を有効活用して、学習の基礎をしっかり固めることで、新学期の授業での理解力や成績アップにつながること間違いありません!オンライン個別指導では、生徒さん一人ひとりの学習進度や理解度に合わせたカスタマイズされた指導が可能です。数学の難しい問題や概念も、分かりやすく丁寧に解説いたします。
また、復習だけでなく、新学期の内容の先取りや苦手な分野の克服にも力を入れています。自信を持って新学期にスタートできるようサポートいたします。
ぜひ、夏休み中に一緒に学習を進めましょう!ココナラ内で私をフォローしてくださった方限定で、初回の体験授業を半額にします!(¥4,000→¥2,000)ご希望の方は、フォローの後にメッセージで連絡をいただけると幸いです。↓中学・高校数学↓中学受験算数ご質問や要望があれば、どんなことでもお気軽にお伝えください。
一緒に学ぶことができるのを楽しみにしています。
0

数学は暗記科目だよって話。
数学は、多くの人にとって難解で難しい学問と感じられることがあります。そのため、多くの人が数学を暗記科目として認識しているかもしれません。実際に、数学は暗記が不可欠な側面があります。
一般的に、数学の学習は公式や定理、公理などの基本的な知識を暗記することから始まります。これらの基礎的な知識を身につけることで、数学の枠組みや論理構造を理解しやすくなります。例えば、初等代数の公式や幾何学の定理、微分積分のルールなどは、暗記していないと問題を解く上で困難になることがあります。
さらに、多くの難関大学の入試問題は、基礎的な知識や公式を駆使して解くことが求められることがあります。入試問題の難易度が高い理由の一つは、問題の背後にある基本的な数学の概念を理解しているかどうかを確かめるためです。入試問題は基礎問題の応用で構成されている場合が多く、基本的な知識がなければ応用問題にも対応しにくくなります。また、数学の学習においては、様々な公式や定理が次々と登場します。これらを暗記しておくことで、問題解決の際にスムーズに利用することができます。問題の解法に時間をかけずに、効率的に解答できるようになるため、暗記力は数学の学習において重要な要素となります。
ただし、数学が暗記科目であるというだけで、理解や応用力が不要だというわけではありません。数学の真髄は論理的思考や問題解決能力にあります。基礎的な知識を暗記した上で、その背後にある論理や理論を理解し、応用する力を養うことが重要です。
数学の学習では、暗記と理解をバランスよく取り入れることが大切です。暗記した知識を活用しつつ、理解力や論理的思考力を養うこと
0

夏休みの授業枠が埋まりつつあります
7月も中旬にさしかかり、学校によっては事実上の夏休みに入ったところも出てきました。そのためか、先週末から新規授業のお問い合わせを10件いただいており、私も驚いています。ただ、7月~8月の授業可能な枠が次第に埋まりつつあります。今後は満枠対応、キャンセル待ちになる可能性も出てきましたので、こちらであらかじめご案内します。オンライン授業を行う祭は、基本的に以下のような流れで対応しています。1. メッセージでお問い合わせいただく↓2. 学習状況や志望校などを確認した上で体験授業の日取りを設定する(最大90分間)。↓3. 体験授業後に授業継続をご希望の場合は、使用テキストや曜日・時間帯を改めて設定↓4. 本格始動開始使用するテキストについてのお問い合わせも頻繁に承っております。学校や塾で使用されているものがあればそちらを、そうでなければ市販教材(公立中高であればチャート式数学、中高一貫校であれば体系数学やAクラス問題集)をお買い求めいただき、授業中はその問題演習をおこないます。また、余力があれば私の方でオリジナルの添削課題をご用意することもできます(オプション価格になります)。ココナラでのオンライン授業を開始して1年に満たないため、対面授業と比較して大幅に割安な価格で授業料を設定してきましたが、昨今の物価の高騰もあり、この秋以降は授業料を改定する場合があります。私の授業をご検討の方は、できるだけお早めにお問い合わせください。
0

“内側” 極限
パッとしないタイトルですがご了承ください。数学をやっていると、たまーに積の極限を考えることってありますよね?a_n → a, b_n → b ならa_n b_n → a bみたいなヤツです。これが成り立つことの証明の中で収束列は添字によらず一様に有界というのを使っているのは、皆様ご存知でしょうか?つまり、ノルム (絶対値みたいなものです) に関しての収束の時でないとこういう積の極限って存在するかも怪しいんですよね。 「 (ノルムから定まるものより) 弱い位相で稠密な集合上結構いい性質が言えてるけど、うまいネット (数列みたいなもの) で性質を全体に飛ばせないかなあ...」そんな時に役に立つのが Kaplansky density theorem というものです。Wikipedia の記事の中で“The density theorem is Kaplansky's great gift to mankind. It can be used every day, and twice on Sundays.”なんて書かれたりしている定理です。大雑把には収束先の内側から収束するようなネット (数列みたいなもの) の存在を言っているのです。皆さんも休みの日は 2 回くらい使ってみましょうね!
0
あなたも記事を書いてみませんか?
多くの人へ情報発信が簡単にできます。
ブログを投稿する
多くの人へ情報発信が簡単にできます。